Brill-Noether theory of random graphs
Brill-Noether theory is the part of classical algebraic geometry that deals with maps from algebraic curves to projective space, and can be reinterpreted in terms of the geometry of an abelian group (the Jacobian of the curve) together with a distinguished generating set (the image of the Abel-Jacobi map). An analogous theory for graphs, with Jacobians and Abel-Jacobi maps and many results linked to classical Brill-Noether theory has emerged in the last five years. The goal of this project is to start investigating the Brill-Noether theory of an Erdos-Renyi random graph. Participants will learn background about Brill-Noether theory, graph Laplacians, Jacobians, and Erdos-Renyi random graphs while working examples by hand and doing computer experiments to gather empirical data. Very little is known in this area, so whatever is discovered will be new.
All-pay bidding games
Bidding games are variations on familiar two-player games, such as chess or Tic-Tac-Toe, in which, rather than alternating moves, the players bid to determine who moves next. There is now a well-developed theory of such games where the bidding is a “first price auction”, i.e. the player who makes the higher bid pays for the move, and the player who makes the lower bid pays nothing. The goal of this project will be to investigate bidding games with a different auction structure, the “all-pay auction”. Both players make a bid, and now both players pay, but only the high bidder gets the move. First price auction bidding games always have deterministic optimal strategies, and these strategies are known for simple games, including Tic-Tac-Toe. However, all-pay bidding games rarely have deterministic optimal strategies – instead, optimal strategies involve bidding randomly according to some optimal distribution. In this sense, all-pay bidding games behave more like the noncooperative games studied by economists and less like the combinatorial games studied more commonly by mathematicians – and a well-developed theory could help bridge the gap between these two parts of the game theory world. Very little is known about all-play bidding games, so whatever is discovered is likely to be new. One ambitious goal would be to determine optimal strategy for all-pay Tic-Tac-Toe.
Integer partitions in number theory and combinatorics
There are five ways to express the number 4 as a sum of positive integers: 4 = 3 + 1 = 2 + 2 = 2 + 1 + 1 = 1 + 1 + 1 + 1 so we say there are five “partitions” of 4, and write p(4)=5. More generally, for any non-negative integer n, we let p(n) := #{partitions of n}. As is often the case in mathematics, natural and seemingly elementary concepts such as counting partitions have led to some very difficult, complex, and beautiful problems and ideas. Within number theory and combinatorics, partitions have been an object of study for centuries, dating back to Euler and Ramanujan, and they are still an area of active research in present day. It is not difficult to realize that the partition numbers grow quickly: for example, p(50) = 204226, p(200) = 3972999029388, and p(1000) > 24 x 10^30. Natural questions to ask are: (1) How fast does p(n) grow, asymptotically, as n tends towards infinity? (2) Given that the prime numbers are the building blocks of all integers, can we understand which primes divide p(n) in terms of n? (3) Could there be an exact formula for p(n) in terms of n? Though these questions are simple and natural to state, their answers are non-trivial, and are intimately linked to some deep ideas. In this project, students will explore some related open problems and conjectures, as well as formulate their own, associated to special families of partition numbers. In the process, students will have the opportunity to learn, use, develop, and expand upon some techniques and ideas from number theory, combinatorics, modular forms, computing, and discrete math.
Core Partitions and Numerical Semigroups
A partition of n is a way of writing n as a sum of positive integers, n = a_1 + a_2 + … + a_k, where a_1 >= a_2 >= … >= a_k >= 1. We can represent a partition by its Ferrers diagram, a left-justified array of boxes where the number of boxes in the mth row is equal to the mth part of the partition. For example, the partition 3+2+2+1+1 of 9 has 3 boxes in its first row, 2 boxes in its second, and so on. Each box in the Ferrers diagram has an associated hook length, the number of boxes directly below it plus the number directly to the right of it, plus one. These hook lengths play an important role in the representation theory of the symmetric group.
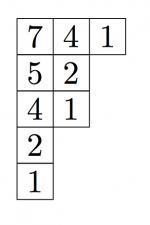
Each box in the figure above is labeled by its hook length. A partition is called a t-core if none of its hook lengths are divisible by t. Given two relatively prime integers s and t, there are only finitely many partitions that are simultaneously s-cores and t-cores. This partition is simultaneously a 3-core and an 8-core, but it is not a 5-core. Several recent papers have studied these simultaneous core partitions. For example, the average size of a simultaneous s/t-core partition is currently unknown.
A numerical semigroup is an additive submonoid of the natural numbers with finite complement. There is a straightforward process to build a partition out of such a semigroup, which gives a method for producing large sets of simultaneous core partitions. In this project students will investigate the properties of this special set of partitions and more general questions about hook sets and cores.
Geometry of Polynomials
Many important problems in mathematics and theoretical computer science have been solved by reducing them to problems about polynomials. Often one is interested in proving that the roots of the polynomials obtained satisfy certain properties. It then helps to understand the operations on polynomials which preserve these properties. Consider a polynomial with real coefficients with the property that all it roots are real. This property of having real roots is preserved under many operations on polynomials, such as taking derivatives. A better understanding of how roots move under these operations turns out to be very useful. A result of this nature was a key ingredient in the recent resolution of the long standing Kadison-Singer problem. In this project, students will explore how natural transformations of polynomials affect the roots of those polynomials.
The toric geometry and combinatorics of graph associahedra
Toric varieties provide a deep and powerful link between algebraic geometry and the combinatorics of convex lattice polytopes. Given a convex lattice polytope P, one builds a projective toric variety X(P) whose geometry is essentially determined by the polytope P. One particularly interesting class of lattice polytopes are graph associahedra, which generalize well-studied objects such as the permutohedron and associahedron. Graph associahedra associate to every connected graph on n vertices an (n-1) dimensional polytope. The goal of this project will be to explore the relationship between the combinatorics of the graph, the convex geometry of the graph associahedron, and the geometry and topology of the variety X(P). A secondary goal might be to determine the relationship between graph associahedra and Hassett’s weighted moduli spaces of curves. Students will learn and explore these problems by working with concrete examples, and by using the extensive SAGE library on toric varieties to test their results and conjectures. Very little seems to be known about this problem, so anything discovered is likely to be new.
