This is the list of projects for 2020. These should each be looked over before applying. The application form is available here and must be filled out by February 15, 2020.
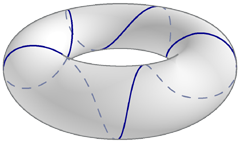
Geodesic nets on flat spaces
In Euclidean space, the shortest path between two points is a straight line. In non-Euclidean spaces, geodesics abstract the notion of a straight line. For example, on the sphere the shortest paths are the great circle geodesics, and we fly “over the pole” when traveling from NYC to Paris. This summer we’ll study geodesic nets: graphs embedded in manifolds such that each edge is a geodesic. We’ll explore the existence and behavior of these nets, focusing on flat spaces where the edges must be straight lines.
Mentor: Ian Adelstein (Yale) and Elijah Fromm (Yale)
Stationary operators for the Toda flow
The Toda flow describes solutions to certain special ordinary differential equations defined initially on one-parameter families of symmetric matrices. The remarkable property of the Toda flow is that solutions are isospectral; that is, the eigenvalues of solutions remain fixed under the flow. Furthermore, the flow converges to a diagonal matrix exponentially fast. For finite matrices, the stationary points (i.e., constant solutions) of the Toda flow are simply diagonal matrices; however, the flow can naturally be extended to infinite tridiagonal matrices, called “Jacobi operators”, which have much more interesting stationary solutions. In this project, we will search for special stationary Jacobi solutions of the Toda flow which are exceptionally rare but of interest in mathematical physics.
Mentor: Tom VandenBoom (Yale)
Toplogical zeta functions of matroids in families
A matroid is a combinatorial object which abstracts the notion of (linear or algebraic) independence. Over the past 5 years, significant progress has been made in matroid theory due to the introduction of new matroid invariants coming from algebraic geometry. One less-studied such invariant is the topological zeta function of a matroid. The topological zeta function Z_M(s) of a matroid M is a rational function in one variable. While some basic properties of Z_M(s) are known (for instance, the first three terms of its Taylor expansion at s=0), it remains largely mysterious precisely what combinatorial data is “stored” in Z_M(s). In this project, we will find simple expressions for the topological zeta functions of several specific families of matroids (for instance, braid matroids, wheel matroids, whirl matroids). We will study various properties of these functions (their Taylor expansions, their zeros and poles), with an eye towards combinatorial interpretations. The ultimate goal will be to conjecture and prove statements about topological zeta functions of general matroids.
Mentors: Max Kutler (Kentucky) and Shiyue Li (Brown)
Graph Laplacians
One way to perform analysis on self-similar fractals, especially studying the heat and wave equations, is to study a sequence of finite graphs which approximate the fractal. Specifically, the sequence of spectra (eigenvalues) and vibration modes (eigenvectors) of the Graph Laplacian matrices can give important information about limiting processes on the fractal. This project will focus on obtaining numerical and theoretical results for families of graphs that approximate self-similar fractals resulting from an iterated function system (IFS). Numerical experimentation and analysis is very useful, and so some coding experience is recommended.
Mentor: Ryan Pellico (Trinity)
Problems in Homogeneous Dynamics
Dynamical systems study the asymptotic behavior of a transformation acting on some kind of mathematical space. Historically, dynamical systems have been used to model natural phenomena, such as the motion of planets or the spread of disease. These models are generally classified as either discrete-time dynamical systems (which can be described by a Z or Z+ action on the underlying space) or continuous dynamical systems (described by an R or R+ action). It turns out that many of the methods used to study such systems can be generalized to study the actions of other groups with a sufficient amount of structure, and doing so can yield valuable insights into areas of pure mathematics, such as number theory and geometry. The field of homogeneous dynamics studies the actions of subgroups of a Lie group G on the quotient of G by a discrete subgroup (recall that a Lie group is a manifold which is also a group, where the group operations of multiplication and inversion are smooth). A typical question in this area is: Given a point x and acting subgroup H, what does the orbit Hx look like inside the space? For an example of this kind of system, one needs look no further than a linear flow on the torus, R^2/Z^2. Consider the left multiplication action of a linear subgroup generated by a nonzero vector v in R^2. It turns out that the orbit of every point is closed and homeomorphic to a circle if and only if the entries of v are rationally dependent, and that the orbit of every point is dense otherwise. As another example, consider the space SL(n,R) of nxn matrices with real coefficients and determinant 1, quotiented by its subgroup SL(n,Z) consisting of matrices with integer coefficients. This space can be identified with the space of unimodular lattices in R^n, and is of great importance in number theory. There are several natural subgroup actions on this space, including the geodesic flow (which can be realized as an action by the diagonal subgroup) and the closely related horocycle flow (the action by upper triangular unipotent matrices). In this project, we will develop the relevant background in ergodic theory and Lie groups to study the distribution of certain orbits and subsets of these orbits within homogeneous spaces such as SL(n,R)/SL(n,Z).
Mentor: Taylor McAdam (Yale) and Caglar Uyanik (Yale)