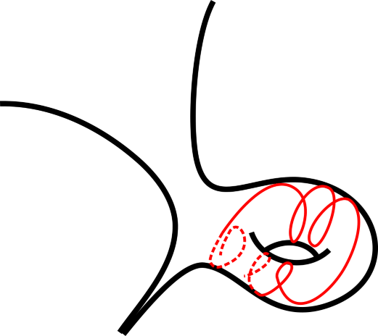Combinatorial and geometric aspects of hyperbolic manifolds
Hyperbolic geometry is important for understanding the geometry and topology of 3-manifolds, largely due to Thurston’s geometrization conjecture. This conjecture, which follows from Perelman’s celebrated work, states that any closed 3-manifold can be canonically decomposed into pieces, each of which corresponds to one of eight geometric model structures, hyperbolic geometry among them. Hyperbolic manifolds exhibit a large variety of behavior, which makes them difficult to understand and classify, as well as fundamental objects of study. Its interaction with 2-dimensional geometry, as well as 2 and 3 dimensional topology, makes it an ideal topic to find accessible problems for undergraduate students while also providing access to key questions in mathematics. This project will look into comparing combinatorial aspects coming from topology with geometric and analytic properties of hyperbolic manifolds of dimension 2 and 3.
Mentor: Franco Vargas Pallete (Yale)
Algebraic Combinatorics
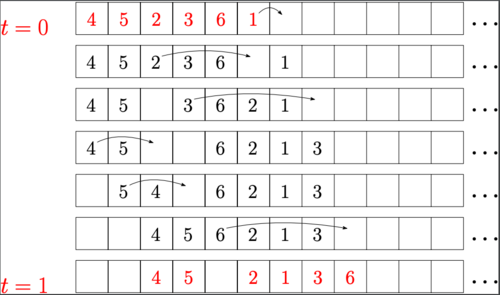
A (multicolor) box-ball system is a discrete dynamical system whose dynamics come from the balls jumping to the first empty box one at a time, starting with the smallest-numbered ball:
Every box-ball system will eventually reach a steady state, decomposing into solitons. In this project, we will use Robinson-Schensted-Knuth (RSK) tableaux to study these solitons. Other potentially helpful concepts include consecutive pattern avoidance in permutations, Motzkin numbers, generating functions, and the weak partial order on the symmetric group.
Cluster algebras are commutative rings with rich combinatorial structure. The theory of cluster algebras is only 21 years old but has connections to diverse areas of mathematics and physics, e.g., representation theory of finite-dimensional algebras, hyperbolic geometry, polytopes, dynamical systems, topology, string theory and (possibly) box-ball systems. A cluster algebra is associated to oriented graphs (called quivers) which are related to one another via a process called mutation. Many facts about quiver mutations have been proven using non-combinatorial techniques coming from the fields mentioned above. We will attempt to give combinatorial explanations to these facts, and then try to make progress on open problems.
Mentor: Emily Gunawan (University of Oklahoma) and Su Ji Hong (Yale)
Geometry and dynamics in H² × H²
A hyperbolic surface is a two-dimensional topological manifold equipped with a complete hyperbolic metric. Such surfaces can be realized as quotients of the hyperbolic plane H² by a discrete group (isomorphic to the fundamental group of the surface). The geodesic flow on a hyperbolic surface describes the free (inertial) motion of a particle bound to that surface. The trajectories of this flow (geodesics) typically exhibit complicated and chaotic behavior, intricately related to the geometry of the ambient surface.
For nice hyperbolic surfaces (a.k.a. geometrically finite), one characteristic property is that all geodesic trajectories are either recurrent (return infinitely often to some compact set) or escape to infinity in a simple way (through one of a finite number of ends of the surface).
In this project we plan to study a higher-rank analogue of this setting, specifically quotients of H² × H² by nice discrete (Anosov) groups of isometries. Our goal is to understand how geodesic trajectories escape to infinity in such spaces.
Mentors: Or Landesberg and Subhadip Dey (Yale)
Extremal problems in discrete geometry
Questions in discrete geometry typically involve finite sets of points, lines, circles, planes, or other simple geometric objects, and many of them are very natural and worth studying for their own sake. Some of them, such as the structure of 3-dimensional convex polytopes, go back to the antiquity, while others are motivated by connections with different areas of modern mathematics, in particular extremal combinatorics, harmonic analysis, number theory, and topology. Every now and then, a new phenomenon is discovered in one place and this leads to surprising progress on all fronts. Over the past several years in particular, several ground-breaking results have been discovered, answering (or nearly answering) some of the oldest problems in the field.
In this REU project we will try to capitalize a little bit on this momentum. We will study a couple of these recent developments in the area, and then aim to make progress on a few new problems. Possible topics could include (but are not limited to): incidence geometry, (hyper)graph theory, Ramsey theory, convex geometry, or coding theory.
Mentor: Cosmin Pohoata (Yale) and Hong Liu (Warwick)
Directed-graph based inference in machine learning
With the advent of high-dimensional, high-throughput data in many fields including biomedicine, social science, physics, finance, etc, there is increasing value in graph-theoretic models of data. Standard methods in network science have focused on undirected graphs. When the inherent connectivity structure in the data is directional, however, application of the standard methods incur loss of information. In order to study directed graphs, people have proposed magnetic Laplacians and more recently effective-resistance based methods. However, these have not been widely incorporated into machine learning and deep learning frameworks. Goals of this project would be to discover new metrics for directed graphs, design algorithms for informative embeddings, and incorporate these into graph neural networks computations to define novel class of methods for graph attention, graph filtering, message passing, and message aggregation.
Mentors: Smita Krishnaswamy, Ian Adelstein, Dhanajay Bhaskar (Yale), and Michael Perlmutter (UCLA)
Application Information
Thanks to new support from the NSF the SUMRY program is now available both to currently enrolled Yale undergraduates AND non-Yale undergraduate students.
SUMRY 2022: May 31 to July 28 - the current plan is in-person at Yale
HOW TO APPLY - first please review the project descriptions below
Yale students - you need only fill out the application form available on the side bar.
Non-Yale students - you need to both fill out the application form on the side bar AND apply via mathprograms. The mathprograms application requires a letter of recommendation from a math faculty member, to be uploaded directly via mathprograms.
We are now accepting applications. The due date for applications is February 3, 2022. Students should expect to hear back from us by the middle of February. Students will need to respond to our invitations by the national REU deadline of March 8, 2022.
All of the projects are meant to be accessible to undergraduate mathematics students. The following descriptions may include terms and ideas with which you are unfamiliar; this is expected, you will learn much of the background during the summer.
SUMRY was supported in part by NSF DMS-1831960.